science
Circuit quantique supraconducteur pour NOR dans le recuit quantique
Caractéristiques de fonctionnement NOR et NAND
NOR est connu pour être une unité de calcul polyvalente. Dans notre méthode, l’hamiltonien est conçu pour réduire la puissance des composants logiques NOR. Le circuit quantique supraconducteur est construit par implémentation directe du circuit hamiltonien illustré sur la figure supplémentaire 1 (a). Deux types d’échantillons constitués de trois qubits correspondant à . sont préparés une Et le B pour la saisie et s Pour le résultat booléen, avec des courants critiques (jec) de 6,25 A (NOR1) et 3,75 A (NOR2). Le modèle de configuration est décrit dans la section « Méthodes ». Composantes booléennes de NOR, correspondant à quatre groupes de (uneEt le BEt le s) avec une puissance minimale, apparaissent au point de dissolution après assurance qualité. Théoriquement, le point de dissolution est exprimé par.
$$ I_{h2} = \frac {{M_{23}}}{{M_{31}}}\cdot I_{h1}$$
Et le
$$ I_{h3} = \frac {{M_{1}}}{{M_{3}}}\cdot\frac {{M_{23}}}{{M_{12}}}\cdot I_{h1 } $$
(1)
où jehje (je = 1–3) est le biais externe du qubit je(correspondant aux étiquettes une Et le B,Et le s ), Mje (je = 1–3) est l’inductance mutuelle entre les qubits jeet la ligne de polarisation externe, et MJE (je= 1–3, y= 1–3) est l’induction mutuelle entre les qubits jeEt le y. Processus de dérivation d’équation. (1) Décrit dans Méthodes supplémentaires. Les inductances des qubits et leurs inductances mutuelles sont extraites du schéma de circuit (voir Méthodes). Les points de décroissance théoriques de NOR1 et NOR2 sont estimés comme (jeh1Et le jeh2Et le jeh3) = (1.4, 1.4, 3.1) et (1.3, 1.3, 2.8) [µA], successivement. Les figures 1a-c montrent respectivement les diagrammes d’état obtenus à partir de la théorie, à partir de simulations utilisant le Josephson Integrated Circuit Simulator (JSIM)27 avec jeh3= 2,0 µA, et d’expérience avec jeh3= 2,0 µA réalisé à 10 mK. Le JSIM détaillé et les méthodes expérimentales sont présentés dans la section Méthodes et dans la section « Configuration expérimentale » des Méthodes supplémentaires, respectivement. Dans l’analyse JSIM, le courant de bruit thermique est négligé afin de mettre l’accent sur la direction de l’état limite dans chaque composant logique. Un point d’arrêt est trouvé, où chaque composant booléen d’un NOR apparaît, sur l’état actuel de (jeh1Et le jeh2 Et le jeh3 ) = (1.8, 1.8, 2.0) [µA] Tant dans les expériences que dans l’analyse JSIM dans NOR1. La figure supplémentaire 3 montre la distribution itérative des composants logiques dans les expériences réalisées au point de dissolution. Des composantes booléennes correspondant à l’énergie minimale hamiltonienne sont générées de manière sélective. Dans le diagramme de cas, la frontière se trouve le long de la direction diagonale, que nous appelons une « échelle » pour plus de commodité. Lorsque l’échelle monte en diagonale vers la gauche jeh3Il diminue à partir du point de dissolution (Fig. 1d-f). D’autre part, une échelle qui monte en diagonale dans la bonne direction est créée lorsque jeh3Il augmente le point de dissolution (Fig. 1g-i). Ces tendances sont qualitativement cohérentes avec la théorie, l’analyse JSIM et les expériences. Au point de décroissance obtenu expérimentalement, les composants logiques du NOR se produisent de manière aléatoire (voir la Fig. 4 supplémentaire et la section «Caractéristiques détaillées du processus NOR» dans la note supplémentaire). Notez que nous pouvons produire un composant logique souhaité en appliquant un courant de compensation approprié (α) contre le point de décroissance. Par exemple, le composant logique de (uneEt le B) = (0, 1) peut être considéré en appliquant le biais de sortie de (jeh1 ‘, jeh2 ′) = (jeh1-α, jeh2+ a). Cela correspond à la dépendance de α le long de la direction diagonale du point de décroissance. En appliquant une valeur appropriée de α, la logique NOR peut être reproduite avec une grande précision (voir Fig. 5 supplémentaire). Nous confirmons que l’injection de flux dans l’un des qubits en adoptant α dans l’état initial restreint l’état des autres qubits car les qubits interagissent les uns avec les autres pour réduire l’énergie après QA. De plus, ce circuit quantique se comporte comme une NAND lorsque jehIl est fourni avec un signe négatif. Dans le tracé d’état NAND, la valeur absolue du point de dégénérescence est presque la même que la valeur de NOR. Les frontières de chaque composant logique sont modifiées par jeh3, Il en va de même pour NOR (voir Fig. 6 supplémentaire et la section «Fonctionnement NAND» dans la note supplémentaire). Chaque composant logique d’une NAND est reproduit avec une probabilité de réussite de 100 % en adoptant une valeur appropriée de α (voir Fig. 7 supplémentaire). QA dans NOR1 montre une forte probabilité de succès dans les opérations NOR et NAND, mais son point de rupture varie entre la théorie, l’analyse JSIM et les expériences.
| Tendances des diagrammes d’état pour le processus NOR. Diagrammes de cas pour (une) jeh3 = 2,0 µA, (défenseur) jeh3 = 1,0 µA, (J) jeh3= 3,0 µA : (uneEt le DocteurEt le F(la théorie,)BEt le eEt le h) Analyse JSIM sans courant de bruit thermique, et (cEt le FEt le jeExpérience 10 mK.
Évaluation de la zone grise
Dans NOR2, la hauteur de barrière dans le potentiel d’énergie par qubit est réduite par rapport à celle dans NOR1 en raison de la réduction de jec. La figure supplémentaire 8 montre la distribution de fréquence pour chaque composant logique avec l’état actuel de (jeh1Et le jeh2 ) = (1.6, 1.6) [µA] et modifier jeh3Entre 0 et 9 A. À propos jeh3A partir de 2,8 µA, tous les composants logiques candidats apparaissent dans le NOR. Les figures 2a, b montrent des diagrammes de cas avec des images 2D et 3D dans jeh3A partir de 2,8 le point de décroissance expérimental est proche du point théorique. Notez que les limites de chaque composant logique changent radicalement autour de ce point. Le point de décroissance empirique de NOR2 est (jeh1 Et le jeh2Et le jeh3 ) = (1.6, 1.6, 2.8) [µA]. Pour plus de commodité, nous définissons la largeur transitoire entre deux régions logiques différentes comme la « région grise ». Il existe deux types de zones grises : le premier type est créé entre des zones adjacentes, telles que « 100 » – « 001 » et « 001 » – « 010 », et le second type se produit dans la même direction diagonale que l’échelle. Théoriquement, la largeur de l’échelle diminue de manière monotone avec le biais externe jeh3avant le point de dégénérescence. Plus tard, il augmente de façon monotone avec jeh3. Les premier et deuxième types peuvent être évalués à partir de quatre types de profils de lignes (L.1 -à4) et profils en L.5 et moi6 , respectivement (Fig. 2c et f). dans L .5 et moi6 , quatre composants logiques de NOR ont été identifiés. Les zones grises de type I dépendent du temps de recuit (June ) (Voir la figure supplémentaire 9 et la section « Fonction de zone grise de type I » de la note supplémentaire). En tant que tel June diminue, l’étendue de la zone grise s’élargit. avec une période plus longue June , l’effet du bruit peut être moyenné dans le temps. Cela contribue à la réduction de la zone grise, ce qui conduit à l’utilisation de l’effet de recuit quantique. Ces zones grises sont illustrées dans le cas de l’analyse JSIM avec courant de bruit thermique (voir Fig. 10 supplémentaire). Les figures 3a, b montrent les zones grises de type I évaluées respectivement dans les expériences et dans l’analyse JSIM. La largeur minimale de la zone grise varie entre les expériences et l’analyse JSIM. L’effet de l’écoulement dû aux cercles environnants apparaît différemment entre le JSIM et les expériences, ce qui se traduit par une différence dans la largeur minimale de la zone grise. Cependant, la prise en compte du pas équidistant courant dans l’évaluation de la zone grise contribue à supprimer l’effet de génération d’une composante logique secondaire. Les zones grises entre ‘100’ et ‘001’ et entre ‘001’ et ‘010’ ont tendance à être significatives. Ces tendances sont cohérentes avec le fait que la situation frontalière est susceptible de changer en raison de jeh3 Dans la figure 1, indiquant la facilité de changer l’état de l’énergie. En revanche, les valeurs sont petites dans les cas limites entre « 110 » et « 010 » et entre « 100 » et « 110 ». Ces tendances sont cohérentes avec le fait que les valeurs de jeh1 Et le jeh2Ne pas changer avec modification jeh3Dans la figure 1, indiquant la difficulté de changer l’état de l’énergie. Ces relations sont également confirmées quelle que soit la valeur de June(Voir la figure supplémentaire 9). Les figures 3c, d montrent une zone grise de type II avec deux orientations dans les expériences et l’analyse JSIM, respectivement. La première est une réponse monotone contre la valeur absolue de jeh3À partir du point de dégénérescence. Cette tendance est conforme aux prédictions de la théorie. La seconde est la zone grise qui s’étend un peu plus large avec des jeh3Avant le point de dissolution de l’augmentation jeh3au-delà du point de dissolution. Ces tendances sont cohérentes avec le résultat illustré à la Fig. 1, où l’occupation de la région ‘001’ est largement modifiée avec une diminution jeh3Par rapport au cas de l’augmentation jeh3. L’analyse JSIM reproduit également les mêmes tendances observées dans les expériences. Notez que les tendances changent pour un courant de bruit thermique supérieur à 2,5 pA/Hz dans l’analyse JSIM. En dessous de 2,0 pA/Hz, un piégeage à l’état minimum local se produit (voir la section « Analyse de la zone grise JSIM » dans les méthodes supplémentaires). La logique dans NOR et NAND peut être obtenue avec une grande précision en ajustant l’état actuel avec des valeurs α supérieures à 1 µA le long d’une direction diagonale à partir du point de décroissance, ce qui contribue à éviter la zone grise.
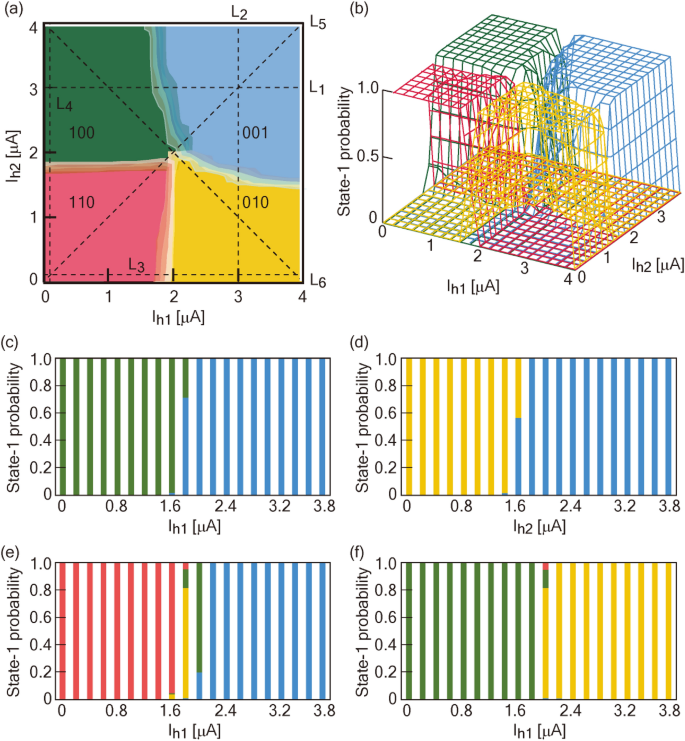
| Analyse des diagrammes d’état dans le processus NOR. (une) deux et (B) Diagrammes d’état 3D de NOR2 dans une expérience de 10 mK jeh3= 2,8 µA. Afin d’analyser la largeur de la frontière entre deux régions logiques (définie comme une zone grise), les profils de ligne de L.1-à6représenté dans (une), est évalué. caractéristiques de ligne de (c) La1(Docteur) je suis2(e) je suis5Et le (F) je suis6.
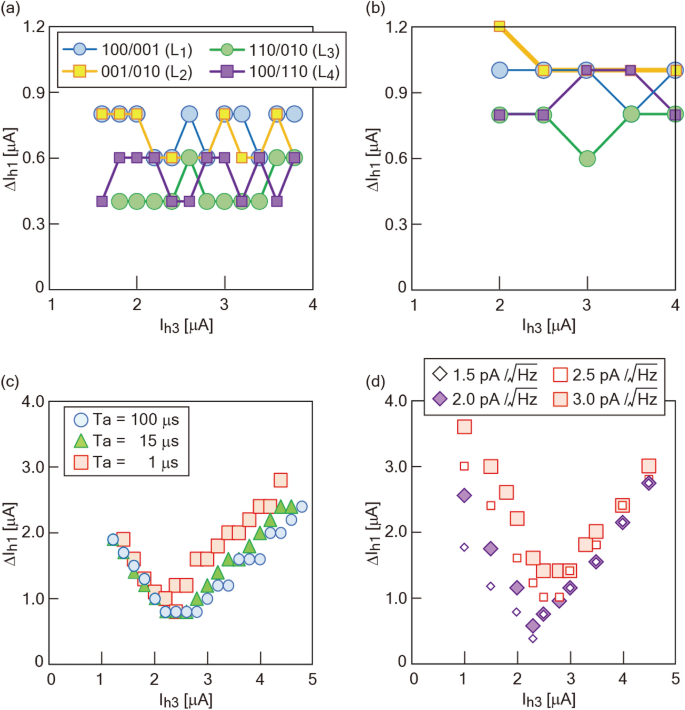
| Analyse de la zone grise. Le premier type d’analyse de zone grise dans (une(Expérience 10 mK)BAnalyse JSIM. encart (une) représente une analyse théorique. Dans l’analyse JSIM pour (B), un courant de bruit thermique de 3,0 pA/√Hz est adopté. Le deuxième type d’analyse de la zone grise dans (c(Expérience 10 mK)DocteurAnalyse JSIM. NOR2 est utilisé.
« Spécialiste de la télévision sans vergogne. Pionnier des zombies inconditionnels. Résolveur de problèmes d’une humilité exaspérante. »
29 août 2024
Le chef du commandement spatial américain espère que la prochaine fois que la Chine lancera un missile laissant derrière elle des débris spatiaux de longue durée, Pékin avertira Washington à l’avance, plutôt que de laisser les États-Unis découvrir par eux-mêmes le chaos orbital.
Parlez dans L’efficacité du Mitchell Institute for Aerospace Studies Lors d’une réunion à la base spatiale Peterson, au Colorado, le 28 août, le général Stephen N. Whiting a souligné deux incidents récents impliquant des débris spatiaux chinois comme étant une source de préoccupation et la nécessité d’améliorer la communication à l’avenir.
« Nous venons de voir le lancement de leur version de Constellation du soleil « Cela a laissé plus de 300 débris en orbite – une fusée Longue Marche 6A », a déclaré Whiting. « Il y a moins de deux ans, ils avaient une autre fusée, qui a mis plus de 500 débris à longue durée de vie… J’espère que la prochaine fois. que « Dans un missile comme celui-ci, il laisse beaucoup de débris. Ce ne sont pas nos capteurs qui détectent cela en premier, mais nous obtenons des communications qui nous aident à comprendre cela, tout comme nous communiquons avec les autres. »
L’incident le plus récent impliquant une fusée Longue Marche 6A s’est produit au début du mois, lorsque le lanceur transportait les 18 premiers satellites d’une constellation de communications prévue pour rivaliser avec Starlink. La fusée s’est brisée en orbite terrestre basse (LEO) quelques jours plus tard, répandant des débris et suscitant des inquiétudes parmi les experts. La société privée de suivi spatial a rapporté que la désintégration pourrait produire plus de 10… 900 épaves shrapnel.
Whiting a noté que les débris provenaient de l’étage supérieur de la fusée après le lancement des satellites, indiquant que la mission était « généralement réussie ». Cependant, à des altitudes plus élevées, les débris resteront en orbite plus longtemps.
« Nous ne voulons certainement pas voir ce genre de débris », a ajouté Whiting.
Les débris se trouvent généralement sur des orbites inférieures à 600 km (373 miles). Il revient sur Terre après quelques annéesÀ une altitude de 800 km, sa décomposition peut prendre des siècles. Avec de plus en plus de satellites en orbite terrestre basse et des débris persistants provenant de lancements peu judicieux, La probabilité de collisions continue d’augmenter.
Selon le général à la retraite Kevin Shelton, directeur du Centre d’excellence sur l’énergie spatiale du Mitchell Institute, les États-Unis ont déjà eu des problèmes similaires avec des débris à haute altitude, mais ont commencé à évacuer le carburant et les gaz des étages de fusée avant d’entrer en orbite. Cette pratique réduisait les débris et le risque de désintégration, et la Russie l’adopta peu après. Whiting a déclaré qu’on ne savait pas actuellement si la Chine utilisait cette méthode.
« Depuis des décennies, les États-Unis s’intéressent tellement à l’espace que nous avons mis la grande majorité de nos données de suivi à la disposition du monde entier », a déclaré Whiting. « Chaque jour, nous analysons tous les satellites actifs à la recherche de tous ces débris, et nous en informons tout le monde, y compris les Chinois et les Russes… parce que nous ne voulons pas que les satellites heurtent des débris et laissent derrière eux d’autres débris. »
Le développement rapide des capacités spatiales et l’augmentation significative des déploiements de satellites par la Chine et la Russie restent une préoccupation majeure quant à la manière dont les États-Unis abordent le domaine spatial. Chef adjoint des opérations spatiales, le général Michael A. Gotlin a souligné que les récentes mesures prises par ces pays prouvent leur intention d’opérer de manière dangereuse dans ce domaine.
« Ils créent beaucoup de débris et d’orbites que nous devons contourner, ou ils mettent en danger des choses comme la Station spatiale internationale », a déclaré Gotlin lors du Sommet AFCEA/INSA sur le renseignement et la sécurité nationale à Rockville, Maryland, le 28 août. Il a ajouté : « Ils ne se soucient même pas de la sécurité des astronautes. Si ce n’est pas dangereux et non professionnel, je ne sais pas ce que c’est. »
En novembre 2021, la Russie a procédé à un test de missile antisatellite, aboutissant à la création d’un Grande quantité de débris En orbite terrestre basse, ce qui présente un danger pour la Station spatiale internationale et incite l’équipage à prendre des mesures de précaution. En outre, Moscou a également été témoin Une série de fuites de liquide de refroidissement Ces dernières années, la Chine a lancé son propre vaisseau spatial. Même s’il n’y a pas de négociations prévues avec la Russie sur le développement spatial, les espoirs sont grands d’une communication plus active avec Pékin sur les alertes spatiales.
« Nous donnons ces avis aux Chinois, et au cours de l’année dernière, nous avons vu à plusieurs reprises qu’ils nous ont donné quelques avis en retour, et je pense que c’est une chose positive. Nous n’avons aucune discussion. prévu avec la Russie », a déclaré Whiting.
« Spécialiste de la télévision sans vergogne. Pionnier des zombies inconditionnels. Résolveur de problèmes d’une humilité exaspérante. »
science
À la recherche de pierres précieuses : caractérisation de six planètes géantes en orbite autour de naines froides
Données d’imagerie à contraste élevé pour toutes les cibles. Dans chaque panneau, nous montrons la limite de contraste de 5σ atteinte en fonction de la séparation angulaire de l’étoile hôte pour chaque ensemble de données à contraste élevé. Nous traçons également des cachets postaux de 1,4″ × 1,4″ d’images NESSI reconstruites en bande z (encadré à droite dans chaque panneau) pour toutes les cibles et des images AO (encarts à gauche) pour TOI-5414, TOI-5616, TOI-5634A et TOI-6034. — astro-ph.EP
Les exoplanètes géantes transitant autour d’étoiles naines de type M (GEMS) sont rares, en raison de la faible masse de leurs étoiles hôtes. Cependant, la couverture de l’ensemble du ciel par TESS a permis d’en détecter un nombre croissant pour permettre des enquêtes statistiques telles que le GEMS Search Survey.
Dans le cadre de cet effort, nous décrivons les observations de six planètes géantes en transit, qui incluent des mesures de masse précises pour deux GEMS (K2-419Ab, TOI-6034b) et une validation statistique de quatre systèmes, qui incluent une vérification et des limites de masse supérieures pour trois d’entre elles. (TOI-5218b, TOI-6034b). 5616b, TOI-5634Ab), tandis que le quatrième système – TOI-5414b – est classé comme « planète potentielle ».
Nos observations incluent les vitesses radiales du Habitable Zone Planet Finder sur le télescope Hobby-Eberly et de l’observatoire Maroon-X sur Gemini-North, ainsi que la photométrie et l’imagerie à contraste élevé provenant de plusieurs installations au sol. En plus de la photométrie TESS, K2-419Ab a également été observé et validé statistiquement dans le cadre de la mission K2 au cours des campagnes 5 et 18, qui fournit des contraintes orbitales et planétaires précises malgré la faible luminosité de l’étoile hôte et la longue période orbitale d’environ 20,4 jours.
Avec une température d’équilibre de seulement 380 K, K2-419Ab est l’une des planètes en transit les plus froides et les mieux caractérisées connues. TOI-6034 a un compagnon tardif de type F à environ 40 secondes d’arc, ce qui en fait la première étoile hôte GEMS à avoir un ancien compagnon binaire sur la séquence principale. Ces confirmations s’ajoutent au petit échantillon existant de planètes en transit GEMS confirmées.
Shubham Kanodia, Arvind F. Gupta, Caleb I. Canas, Lea Marta Bernabo, Varghese Reggie, T. Hahn, Madison Brady, Andreas Seyfart, William D. Cochrane, Nydia Morrell, Ritvik Basant, Jacob Bean et Chad F. Bender, Zoé L. De Bors, Alison Perella, Alexina Birkholz, Nina Brown, Franklin Chapman, David R. Ciardi, Catherine A. Clark, Ethan J. Cotter, Scott A. Diddams, Samuel Halverson, Susan Hawley, Leslie Hebb, Ray Holcomb, Steve B. Howell, Henry A. Kobolnicki, Adam F. Kowalski, Alexander Larsen, Jessica Libby Roberts, Andrea S. J. Lin, Michael B. Lund, Raphael Locke, Andrew Munson, Joe B. Ninan, Brooke A. Parker, Nishka Patel, Michael Rudrak, Gabrielle Ross, Arpita Roy, Christian Schwab, Jomundur Stefansson, Aubrey Thoms, Andrew Vanderberg
Commentaires : Accepté dans AJ
Sujets : Astrophysique terrestre et planétaire (astro-ph.EP)
Citer ce qui suit : arXiv:2408.14694 [astro-ph.EP] (ou arXiv :2408.14694v1 [astro-ph.EP] (pour cette version)
https://doi.org/10.48550/arXiv.2408.14694
Concentrez-vous pour en savoir plus
Date de publication
De : Shubham Kanodia
[v1] Lundi 26 août 2024, 23:47:24 UTC (5 169 Ko)
https://arxiv.org/abs/2408.14694
Astrobiologie
« Spécialiste de la télévision sans vergogne. Pionnier des zombies inconditionnels. Résolveur de problèmes d’une humilité exaspérante. »
science
La Federal Aviation Administration des États-Unis a immobilisé les fusées Falcon 9 de SpaceX dans l’attente d’une enquête sur un rare accident d’atterrissage au large des côtes.
La Federal Aviation Administration a immobilisé les fusées Falcon 9 de SpaceX en attendant une enquête visant à déterminer pourquoi le propulseur du premier étage s’est arrêté. Collision avec un bateau de débarquement tôt mercredi après avoir contribué au lancement d’un autre lot de satellites Internet Starlink.
après Se lever Après avoir reporté mardi soir le lancement du vaisseau spatial avec équipage Polaris Dawn en raison de prévisions météorologiques à long terme défavorables, SpaceX a continué à travailler sur le premier des lancements consécutifs de satellites Starlink, un depuis la Floride et un depuis la Californie.
Mais le deuxième vol a été annulé après que le premier étage utilisé lors du lancement en Floride s’est brisé et est tombé dans l’océan Atlantique alors qu’il tentait d’atterrir sur un drone SpaceX stationné à des centaines de kilomètres au nord-est de Cap Canaveral.
EspaceX
La FAA a déclaré qu’elle ordonnerait une enquête, immobilisant efficacement les fusées Falcon 9 de SpaceX – y compris la fusée Polaris Dawn – jusqu’à ce que l’enquête soit terminée et que les mesures correctives soient approuvées.
« Le retour en vol de la fusée Falcon 9 dépend de la détermination par la FAA que tout système, processus ou procédure lié à l’anomalie n’a pas d’impact sur la sécurité publique », a déclaré la FAA dans un communiqué.
« En outre, SpaceX devra peut-être demander et obtenir l’approbation de la FAA pour modifier sa licence qui inclut des actions correctives et satisfaire à toutes les autres exigences de licence », a ajouté l’agence.
Mardi soir, SpaceX a reporté un lancement prévu mercredi Mission Aube PolarisLe lancement d’un vol commercial comprenant la première sortie dans l’espace par une organisation non gouvernementale a été reporté à vendredi au plus tôt en raison des conditions météorologiques attendues à la fin de la mission. Le lancement a été suspendu indéfiniment dans l’attente d’une enquête sur l’accident à l’atterrissage.
L’échec de l’atterrissage a mis fin à une séquence de 267 récupérations consécutives réussies de boosters remontant à février 2021. Cependant, le deuxième étage de la fusée Falcon 9 a réussi à transporter 21 satellites Starlink sur leur orbite prévue.
L’atterrissage du premier étage semblait normal jusqu’au moment de l’atterrissage, lorsque plus de flammes que d’habitude sont apparues autour de la base de la fusée à l’approche du pont de la fusée. L’une des jambes d’atterrissage s’est effondrée immédiatement après l’atterrissage et la fusée d’appoint, masquée par le feu et la fumée, s’est renversée par-dessus le côté de la péniche de débarquement dans l’océan Atlantique.
EspaceX
EspaceX
EspaceX
« Après une ascension réussie, le premier étage d’une fusée Falcon 9 s’est retourné après son atterrissage sur le vaisseau spatial sans pilote ‘Zero Gravity' », SpaceX Il a dit sur les réseaux sociaux« Les équipes évaluent les données de vol et l’état du missile. »
Il s’agissait du 23e premier étage de la fusée B1062, qui s’est avéré être son dernier lancement et atterrissage, un nouveau record de réutilisabilité. SpaceX autorise les premiers étages de la fusée Falcon 9 pour un maximum de 40 vols par étage.
Peu de temps après le déploiement des satellites Starlink en Floride, la société a annulé le lancement en Californie, qui était prévu à 5 h 58 HAE, pour donner aux ingénieurs plus de temps pour examiner la télémétrie et les séquences vidéo, à la recherche de tout signe de problème. affecter d’autres missiles.
« Retrait de notre deuxième lancement @Starlink la nuit pour donner à l’équipe le temps d’examiner les données d’atterrissage du booster du lancement précédent », a déclaré SpaceX. Il a dit« Une nouvelle date de lancement cible sera partagée une fois disponible. »
« Spécialiste de la télévision sans vergogne. Pionnier des zombies inconditionnels. Résolveur de problèmes d’une humilité exaspérante. »
-
entertainment2 ans agoDécouvrez les tendances homme de l’été 2022
-
Top News2 ans agoFestival international du film de Melbourne 2022
-
science3 ans agoÉcoutez le « son » d’un vaisseau spatial survolant Vénus
-
Tech2 ans ago
Voici comment Microsoft espère injecter ChatGPT dans toutes vos applications et bots via Azure • The Register
-
Tech3 ans ago
F-Zero X arrive sur Nintendo Switch Online avec le multijoueur en ligne • Eurogamer.net
-
science3 ans ago
Les météorites qui composent la Terre se sont peut-être formées dans le système solaire externe
-
Top News2 ans agoComment parier sur le basket : tous les conseils pour continuer et s’amuser
-
entertainment2 ans ago
Seven révèle son premier aperçu du 1% Club
